1、解析几何指借助笛卡尔坐标系,由笛卡尔、费马等数学家创立并发展。它是用代数方法研究几何对象之间的关系和性质的一门几何学分支,亦叫做坐标几何。
2、解析几何包括平面解析几何和立体解析几何两部分。平面解析几何通过平面直角坐标系,建立点与实数对之间的一一对应关系,以及曲线与方程之间的一一对应关系,运用代数方法研究几何问题,或用几何方法研究代数问题。17世纪以来,由于航海、天文、力学、经济、军事、生产的发展,以及初等几何和初等代数的迅速发展,促进了解析几何的建立,并被广泛应用于数学的各个分支。在解析几何创立以前,几何与代数是彼此独立的两个分支。解析几何的建立第一次真正实现了几何方法与代数方法的结合,使形与数统一起来,这是数学发展史上的一次重大突破,作为变量数学发展的第一个决定性步骤,解析几何的建立对于微积分的诞生有着不可估量的作用。

在解析几何中,首先是建立坐标系。取定两条相互垂直的、具有一定方向和度量单位的直线,叫做平面上的一个直角坐标系oxy.利用坐标系可以把平面内的点和一对实数(x,y)建立起一一对应的关系。除了直角坐标系外,还有斜坐标系、极坐标系、空间直角坐标系等等。在空间坐标系中还有球坐标和柱面坐标。
坐标系将几何对象和数、几何关系和函数之间建立了密切的联系,这样就可以对空间形式的研究归结成比较成熟也容易驾驭的数量关系的研究了。用这种方法研究几何学,通常就叫做解析法。这种解析法不但对睁嫌于解析几何是重要的,就是对于几何学的各个分支的研究也是十分重要的。
解析几何的创立,引入了一系列新的数学概念,特别蚂脊是将变量引入数学,使数学进入了一个新的发展时期,这就闷早渗是变量数学的时期。解析几何在数学发展中起了推动作用。恩格斯对此曾经作过评价“数学中的转折点是笛卡尔的变数,有了变书,运动进入了数学;有了变数,辩证法进入了数学;有了变数,微分和积分也就立刻成为必要的了,……”
主要有:椭圆双曲线抛物线三大块,联立方程求解
在高中的话,解析几何 就是 圆锥曲线(包括圆、椭圆、双曲线、抛物线)
解析几何学 是一门高深的学问了啊
解析几何学
时间:2003年8月19日 浏览:1530次 文字大小:大、中、小 打印
解析几何学(analytic geometry)是借助坐标系,用代数方法研究几何对象之间的关系和性质的一门几何学分支,亦叫坐标几何。由法国数学家笛卡儿和费马等人创建,其思想来源可上溯到公元前两千年。
美索不达米亚地区的巴比伦人已能用数字表示一 点到另一个固定点、直线或物体的距离,已有原始坐标思想。公元前4世纪中古希腊数学家门奈赫莫斯发 现了圆锥截线,并对这些曲线的性质做了系统阐述。公元前200年左右阿波罗尼奥斯着有《圆锥曲线论》 8卷,全面论述了圆锥曲桐核线的各种性质,其中采用过一种「坐标」,以圆锥体底面的直径作为横坐标,过 顶点的垂线作为纵坐标,加之所研究的内容,可以看作是解析几何的萌芽。到16世纪末,法国数学家韦达 提出了用代数方法解几何问题的想法,他的思想给笛卡儿很大的启发。此外开普勒发现行星运动三大定律,伽利略研究抛射体运动轨迹,都要求数学从运动变 化的观点研究和解决问题,促进了解析几何学的建立。
1637年笛卡儿出版了一部哲学著作《科学中正确 运用理性和追求真理的方法论》,书中有三个附录,其中之一是《几何学》3卷。这是笛卡儿唯一的数学 论着,阐述了他关于解析几何的思想,后人把它作为解析几何的起点。书中第一次出现变量与函数概念, 他所谓的变量是指具有变化长度和不变方向的线段,还指连续经过坐标轴上所有点的数字变量,因此他试 图创建一种几何与代数互相渗透的学科。在卷Ⅰ中将几何问题化为代数问题,提出几何问题的统一作图法,将线段与数量联系起来,设立方程,根据方程的解所表示的线段间的关系进行作图。卷Ⅱ将平面上的点与一种斜坐标确定的数对联系起来,进一步考虑含两个未知数的二次滑轮禅不定分程,指出它代表平面上的一条曲线,并依据方程的次数将曲 线分类。这样,一个代数方程可以通过几何直观方法去处理,反之可以用代数方法研究曲线的性质,体现了具有某种性质的点之间有某种关系,构成解析几何 的基本思想。
与笛卡儿同代的数学家费马独立发现了解析几何 基本原理。费马在研究阿波罗尼奥斯著作时发现,如果通过坐标系把代数用于几何,轨迹的研究就易于进 行,后为此写了一篇短文《平面与立体轨迹引论信尘》( 1679年发表),其中断言,两个未知量决定一个方程 式,对应着一条轨迹,可以描绘一条直线或曲线。 1643年他又在一封信中描述了三维解析几何的思想。 另一位数学家拉伊尔于1670年也对三维解析几何做过讨论。
解析几何建立后得迅速发展,并广泛用于各个数 学分支。意大利数学家卡瓦列里最先使用极坐标来求阿基米德螺线下的面积。牛顿则第一个把极坐标看成 是确定平面上点的位置的一种方法。18世纪克莱罗在《关于双重曲率曲线的研究》(1731)、欧拉在《无 穷分析引论》(1748)中以及拉格朗日(1773)等都讨论了曲面和空间曲线的解析理论。19世纪德国数学 家普吕克发表《解析几何的发展》(1828-1831)和《解析几何系统》(1835),以优美的方式证明了该 领域中的许多结论和定理,在解析几何发展史上占有重要位置。解析几何学大大推动了微积分学的发展, 也促进了几何本身的进步,它的直接推广还产生了代数几何分支。在解析几何中,「坐标」一词由莱布尼 兹于1692年首先创用。「纵坐标」是他两年后正式使用,「横坐标」到18世纪由德国数学家沃尔夫引用。 而「解析几何学」这个名称直到18世纪末才由法国数学家拉克鲁瓦正式使用。
解析,两个字合起来就是:拆解+分析
将某个(些)不明显的、不容易理解的、不容易宽培友慎槐计算的东西,用明朗的、简单的、容易计算的方式表达出来,这就叫做解析。
函数f(x),我们知道他是个函数,但怎么算?光知道这个不行,f(x)=x²+1,这样就明朗了,能计算了,这是函数的解析式。
一个双曲线,虽然一目了然,但我们并不知道在某一点中庆的具体位置,只知大概,不容易计算,绘制也容易出错,用方程表达出来,y=1/x,就容易计算了,这就是解析几何。
声明: 我们致力于保护作者版权,注重分享,被刊用文章因无法核实真实出处,未能及时与作者取得联系,或有版权异议的,请联系管理员,我们会立即处理,本站部分文字与图片资源来自于网络,转载是出于传递更多信息之目的,若有来源标注错误或侵犯了您的合法权益,请立即通知我们(管理员邮箱:daokedao3713@qq.com),情况属实,我们会第一时间予以删除,并同时向您表示歉意,谢谢!

 999+
999+ 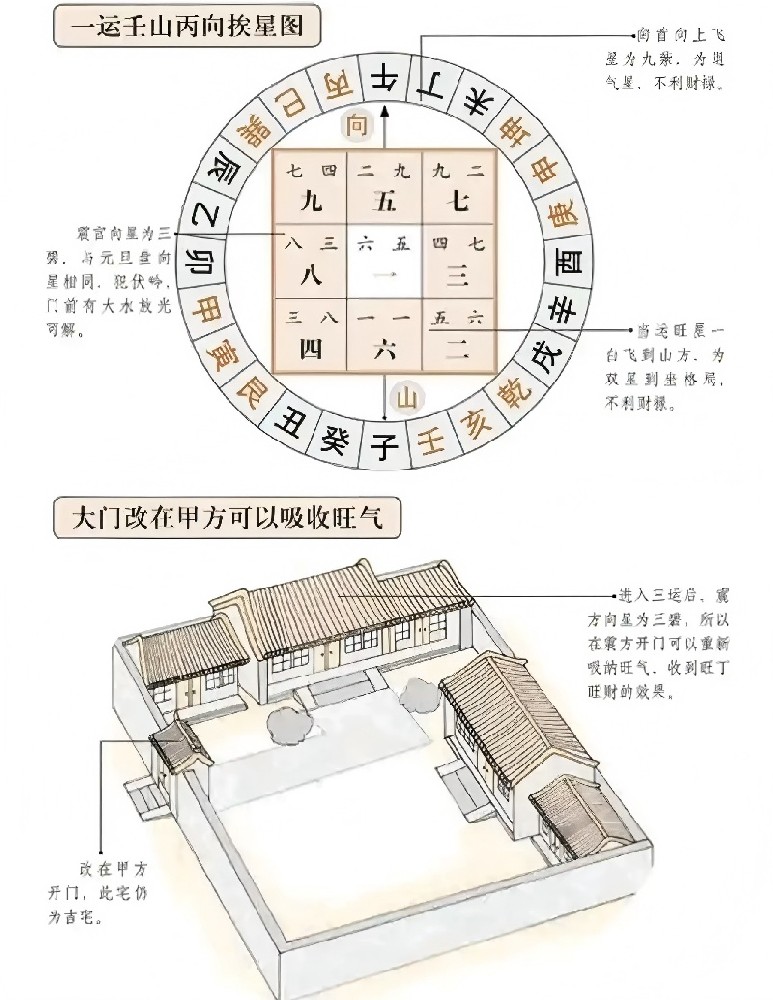
 13
13 
 1843
1843 
 1922
1922 
 1576
1576 
 1961
1961 
 1481
1481 
 833
833 
 689
689 
 1540
1540 本站内容仅供参考,不作为诊断及医疗依据,如有医疗需求,请务必前往正规医院就诊
祝由网所有文章及资料均为作者提供或网友推荐收集整理而来,仅供爱好者学习和研究使用,版权归原作者所有。
如本站内容有侵犯您的合法权益,请和我们取得联系,我们将立即改正或删除。
Copyright © 2022-2023 祝由师网 版权所有
邮箱:daokedao3713@qq.com